Lecture 18 --- Trees, Part I
Review from Lecture 17
- STL set container class (like STL map, but without the pairs!)
- set iterators, insert, erase, find
Today’s Lecture
- Binary trees, binary search trees
- Implementation of ds_set class using binary search trees
Overview: Lists vs Trees vs Graphs
- Trees create a hierarchical organization of data, rather than the linear organization in linked lists (and arrays and vectors).
- Binary search trees are the mechanism underlying maps & sets (and multimaps & multisets).
- Mathematically speaking: A graph is a set of vertices connected by edges. And a tree is a special graph that has no cycles. The edges that connect nodes in trees and graphs may be directed or undirected.
18.1 Definition: Binary Trees
- A binary tree (strictly speaking, a “rooted binary tree”) is either empty or is a node that has pointers to two binary trees.
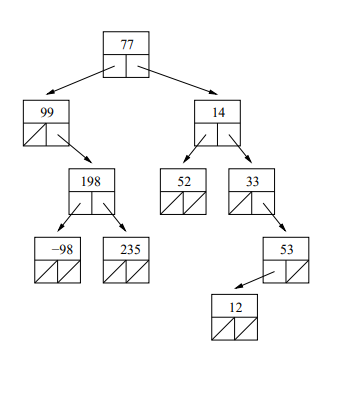
- Here’s a picture of a binary tree storing integer values. In this figure, each large box indicates a tree node, with the top rectangle representing the value stored and the two lower boxes representing pointers. Pointers that are null are shown with a slash through the box.
- The topmost node in the tree is called the root.
- The pointers from each node are called left and right. The nodes they point to are referred to as that node’s (left and right) children.
- The (sub)trees pointed to by the left and right pointers at any node are called the left subtree and right subtree of that node.
- A node where both children pointers are null is called a leaf node.
- A node’s parent is the unique node that points to it. Only the root has no parent.
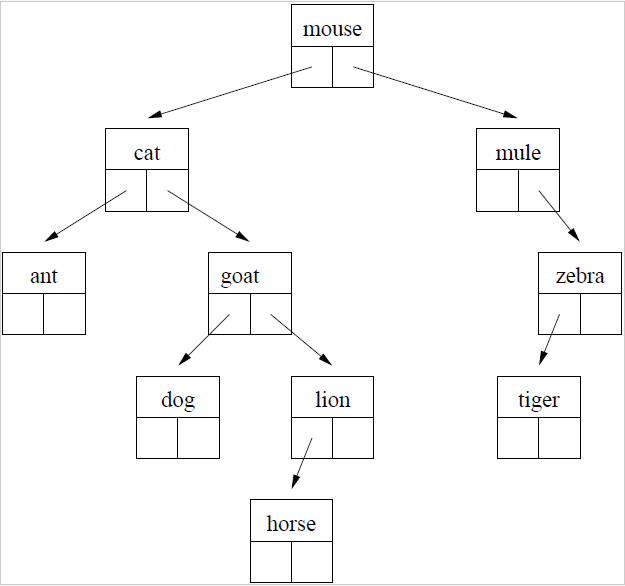
18.2 Definition: Binary Search Trees
-
A binary search tree (often abbreviated to BST) is a binary tree where at each node of the tree, the value stored at the node is – greater than or equal to all values stored in the left subtree, and
– less than or equal to all values stored in the right subtree.
-
Here is a picture of a binary search tree storing string values.
18.3 Definition: Balanced Trees
- The number of nodes on each subtree of each node in a “balanced” tree is approximately the same. In order to be an exactly balanced binary tree, what must be true about the number of nodes in the tree?
- In order to claim the performance advantages of trees, we must assume and ensure that our data structure remains approximately balanced. (You’ll see much more of this in Intro to Algorithms!)
18.4 Exercise
Consider the following values: 4.5, 9.8, 3.5, 13.6, 19.2, 7.4, 11.7
-
Draw a binary tree with these values that is NOT a binary search tree.
-
Draw two different binary search trees with these values. Important note: This shows that the binary search tree structure for a given set of values is not unique!
-
How many exactly balanced binary search trees exist with these numbers? How many exactly balanced binary trees exist with these numbers?
18.5 Beginning our implementation of ds_set: The Tree Node Class
- Here is the class definition for nodes in the tree. We will use this for the tree manipulation code we write.
template <class T> class TreeNode {
public:
TreeNode() : left(NULL), right(NULL) {}
TreeNode(const T& init) : value(init), left(NULL), right(NULL) {}
T value;
TreeNode* left;
TreeNode* right;
};
18.6 Exercises
- Write a templated function to find the smallest value stored in a binary search tree whose root node is pointed to by p.
template <class T>
const T& find_smallest (TreeNode <T>* root)
{
if(root->left == NULL)
{
return root->value;
}
return find_smallest(root->left);
}
- Write a function to count the number of odd numbers stored in a binary tree (not necessarily a binary search tree) of integers. The function should accept a TreeNode pointer as its sole argument and return an integer. Hint: think recursively!
int count_odd (TreeNode<int>* int)
{
if(node == nullptr)
{
return 0;
}
return abs(node->value % 2) + count_odd(node->left) + count_odd(node->right);
}
18.7 ds_set and Binary Search Tree Implementation
- A partial implementation of a set using a binary search tree is provided in this ds_set_starter.h.
- We will use this as the basis both for understanding an initial selection of tree algorithms and for thinking about how standard library sets really work.
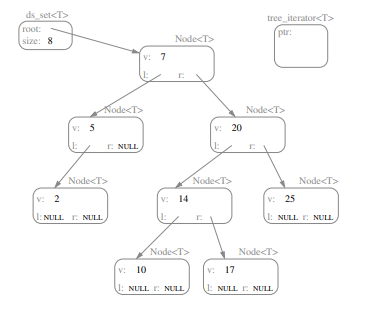
18.8 ds_set: Class Overview
-
There is two auxiliary classes, TreeNode and tree_iterator. All three classes are templated.
-
The only member variables of the ds_set class are the root and the size (number of tree nodes).
-
The iterator class is declared internally, and is effectively a wrapper on the TreeNode pointers.
– Note that operator* returns a const reference because the keys can't change.
– The increment and decrement operators are missing (we'll fill this in next week in lecture!).
-
The main public member functions just call a private (and often recursive) member function (passing the root node) that does all of the work.
-
Because the class stores and manages dynamically allocated memory, a copy constructor, operator=, and destructor must be provided.
18.9 Exercises
-
Provide the implementation of the member function ds_set::begin. This is essentially the problem of finding the node in the tree that stores the smallest value.
-
Write a recursive version of the function find.