Lecture 20 --- Trees, Part III
Review from Lecture 18 & 19
- Overview of the ds_set implementation
- begin, find, destroy_tree, insert
- In-order, pre-order, and post-order traversal;
- Iterator implementation. Finding the in order successor to a node: add parent pointers or add a list/vector/stack of pointers to the iterator.
Today’s Lecture
- Second approach of iterator increement/decrement operator
- Last piece of ds_set: removing an item, erase
- Breadth-first and depth-first tree search
20.1 ds_set Warmup/Review Exercises
- Draw a diagram of a possible memory layout for a ds_set containing the numbers 16, 2, 8, 11, and 5. Is there only one valid memory layout for this data as a ds_set? Why?
- In what order should a forward iterator visit the data? Draw an abstract table representation of this data (omits details of TreeNode memory layout).
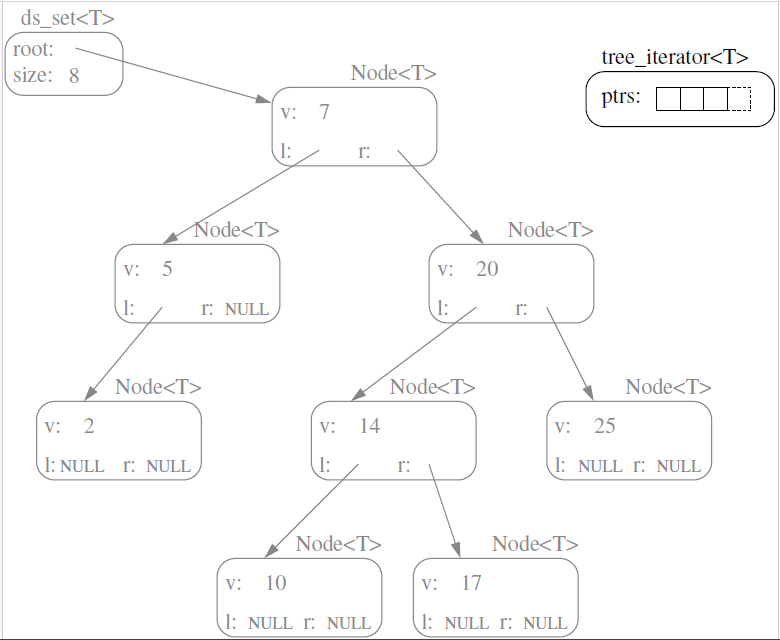
20.2 Second Approach of Operator++
We can also implement operator++ for the ds_set iterator without using the parent pointers. To achieve this, we need a container of pointers representing path from root to node. The following diagram represents the idea, and the code is provided here: ds_set_ptrs.h and ds_set_main.cpp.
20.3 Erase
- First we need to find the node to remove. Once it is found, the actual removal is easy if the node has no children or only one child. Draw picture of each case!
- It is harder if there are two children:
-
Find the node with the greatest value in the left subtree or the node with the smallest value in the right subtree.
-
The value in this node may be safely moved into the current node because of the tree ordering.
-
Then we recursively apply erase to remove that node — which is guaranteed to have at most one child.
-
Play this animation to understand how this works.
- An erase function is provided here:
void eraseHelper(const T& key, TreeNode<T>*& root){
if (root == NULL) return;
if (root->key == key) {
if (root->left == NULL && root->right == NULL){
// no child, just delete
delete root;
root = NULL;
} else if (root->left == NULL){
// doesn't have a left, let the right child take over
TreeNode<T>* temp = root;
root = root->right;
delete temp;
} else if (root->right == NULL){
// doesn't have a right, let the left child take over
TreeNode<T>* temp = root;
root = root->left;
delete temp;
} else {
// has both left and right
// let the leftmost node of the right subtree take over
TreeNode<T>* tmp = root->right;
while (tmp->left) {
tmp = tmp->left;
}
root->key = tmp->key;
// but then remove that leftmost node of the right subtree.
eraseHelper(tmp->key, root->right);
}
} else if (root->key > key) {
// search on the left subtree and erase
eraseHelper(key, root->left);
} else {
// search on the right subtree and erase
eraseHelper(key, root->right);
}
}
Exercise: How does the order that nodes are deleted affect the tree structure? Starting with a mostly balanced tree, give an erase ordering that yields an unbalanced tree.
20.4 Depth-first vs. Breadth-first Search
-
We should also discuss two other important tree traversal terms related to problem solving and searching.
-
In a depth-first search, we greedily follow links down into the tree, and don’t backtrack until we have hit a leaf. When we hit a leaf we step back out, but only to the last decision point and then proceed to the next leaf. This search method will quickly investigate leaf nodes, but if it has made an “incorrect” branch decision early in the search, it will take a long time to work back to that point and go down the “right” branch.
-
In a breadth-first search, the nodes are visited with priority based on their distance from the root, with nodes closer to the root visited first. In other words, we visit the nodes by level, first the root (level 0), then all children of the root (level 1), then all nodes 2 links from the root (level 2), etc. If there are multiple solution nodes, this search method will find the solution node with the shortest path to the root node. However, the breadth-first search method is memory-intensive, because the implementation must store all nodes at the current level – and the worst case number of nodes on each level doubles as we progress down the tree!
-
-
Both depth-first and breadth-first will eventually visit all elements in the tree.
-
Note: The ordering of elements visited by depth-first and breadth-first is not fully specified.
-
In-order, pre-order, and post-order are all examples of depth-first tree traversals. Note: A simple recursive tree function is usually a depth-first traversal.
-
What is a breadth-first traversal of the elements in our sample binary search trees above?
-
20.5 General-Purpose Breadth-First Search/Tree Traversal
- Write an algorithm to print the nodes in the tree one tier at a time, that is, in a breadth-first manner.
// the breadth-first traversal function using std::queue
void breadth_first_traverse(Node* root) {
if (root == NULL) {
return;
}
std::queue<Node*> node_queue; // queue to store nodes for BFS traversal
node_queue.push(root); // start by pushing the root node
int level = 0;
while (!node_queue.empty()) {
int level_size = node_queue.size(); // number of nodes at the current level
std::cout << "level " << level << ": ";
for (int i = 0; i < level_size; i++) {
Node* current_node = node_queue.front(); // get the front node
node_queue.pop(); // remove the node from the queue
std::cout << current_node->value << " "; // print the value of the node
// push the children of the current node to the queue (if they exist)
if (current_node->left != NULL) {
node_queue.push(current_node->left);
}
if (current_node->right != NULL) {
node_queue.push(current_node->right);
}
}
// after we finish the for loop, the only pointers in the queue, are the pointers pointing to nodes of the next level.
std::cout << std::endl;
level++;
}
}
-
What is the best/average/worst-case running time of this algorithm? What is the best/average/worst-case memory usage of this algorithm? Give a specific example tree that illustrates each case.
-
Run this bfs_main.cpp program to test the above function.
-
Play this animation to understand how this works.