CSCI-1200/lectures/21_trees_IV

Lecture 21 --- Trees, Part IV

Review from Lecture 19

• Breadth-first and depth-first tree search
• Increement/decrement operator
• Tree height, longest-shortest paths, breadth-first search
• Last piece of ds_set: removing an item, erase
• Erase with parent pointers, increment operation on iterators
• Limitations of our ds set implementatioN

Today’s Lecture

• Red Black Trees
• B+ Trees

21.1 Red-Black Trees

In addition to the binary search tree properties, the following red-black tree properties are maintained throughout all modifications to the data structure:

• Each node is either red or black.
• The NULL child pointers are black.
• Both children of every red node are black.
• Thus, the parent of a red node must also be black.
• All paths from a particular node to a NULL child pointer contain the same number of black nodes.

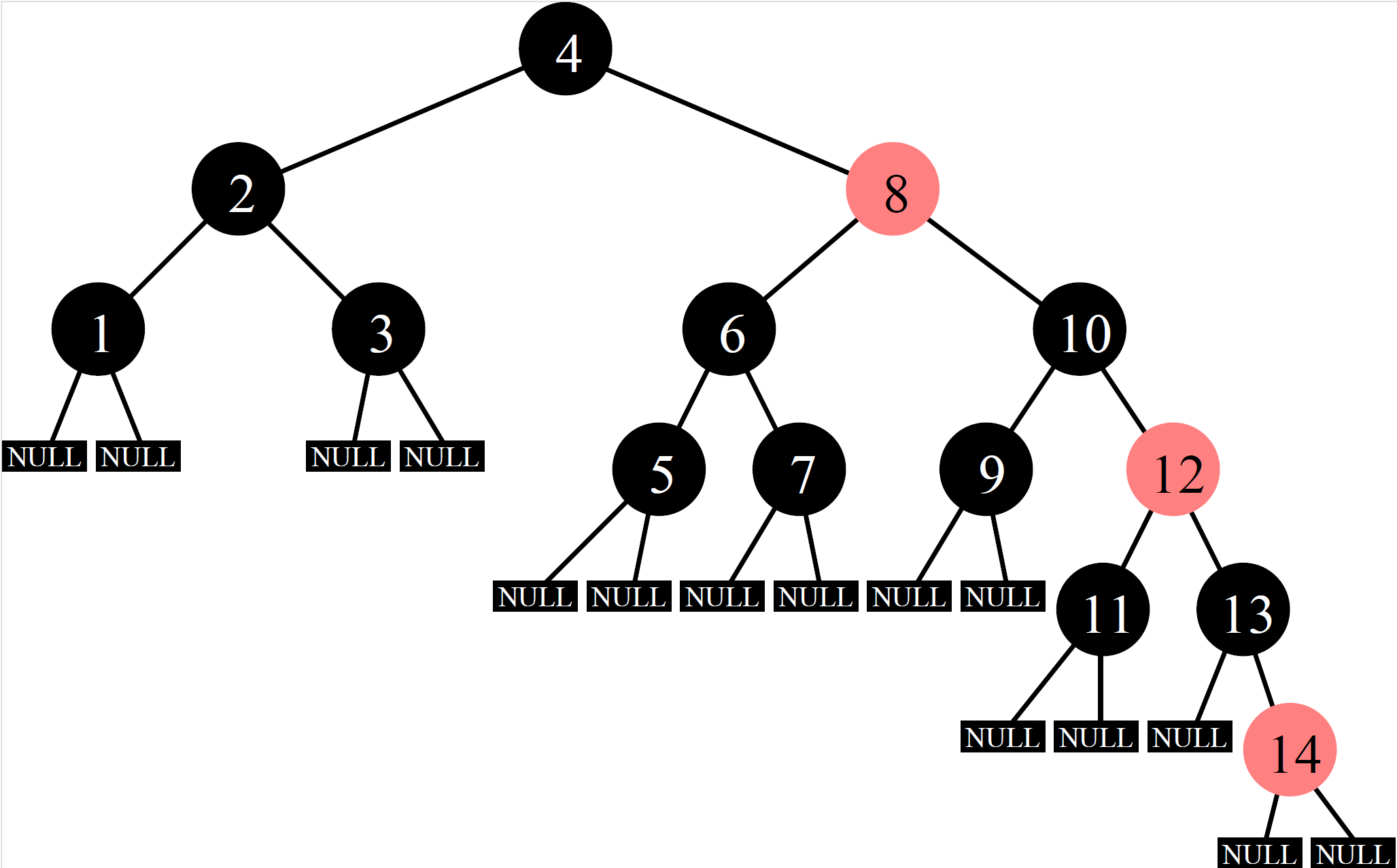
What tree does our ds_set implementation produce if we insert the numbers 1-14 in order?

The tree at the right is the result using a red-black tree. Notice how the tree is still quite balanced.

Visit these links for an animation of the sequential insertion and re-balancing:

http://babbage.clarku.edu/~achou/cs160fall03/examples/bst_animation/RedBlackTree-Example.html

https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

http://www.youtube.com/watch?v=vDHFF4wjWYU&noredirect=1

What is the best/average/worst case height of a red-black tree with n nodes?

           

What is the best/average/worst case shortest-path from root to leaf node in a red-black tree with n nodes?

           

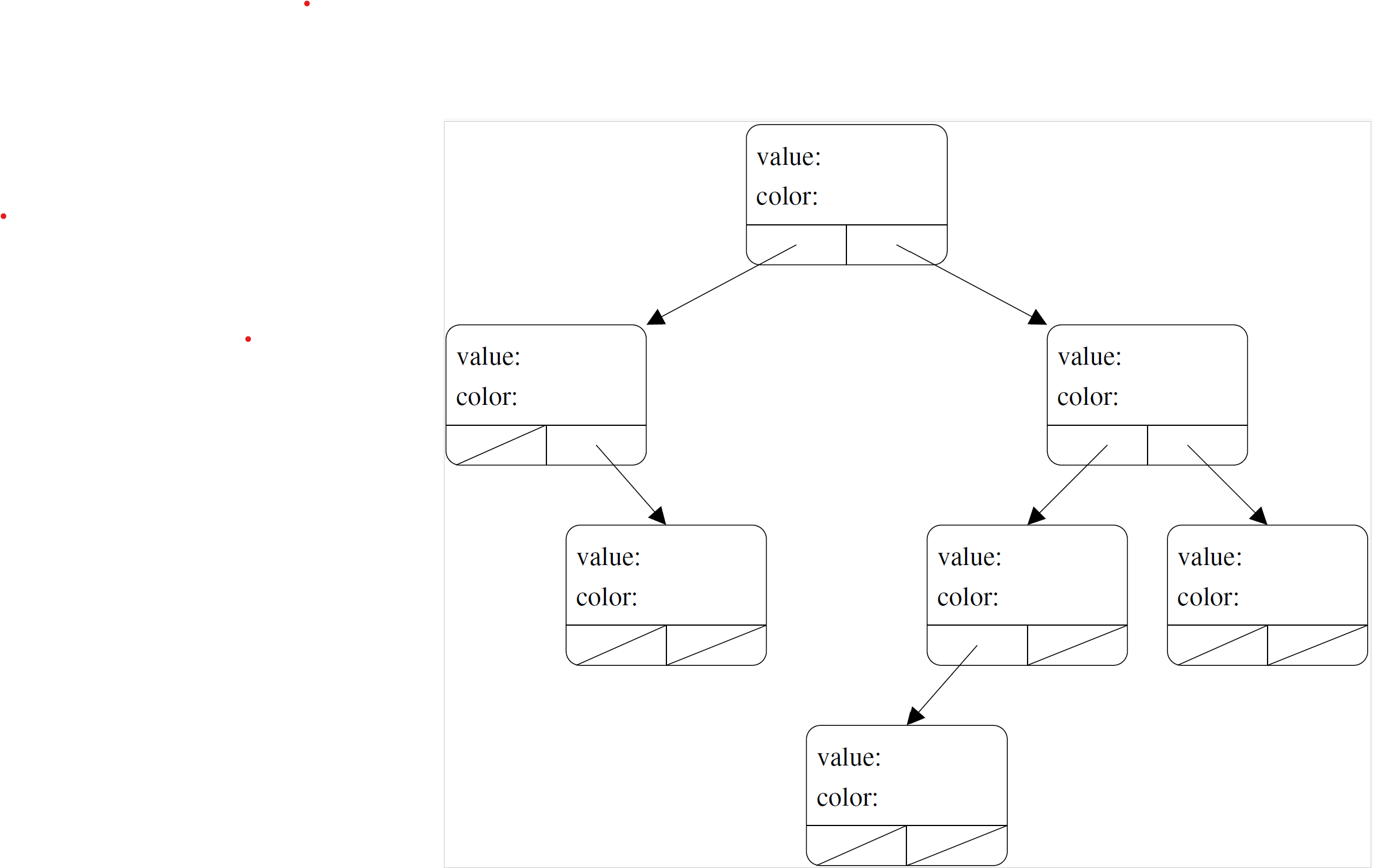
Exercise 21.2

Fill in the tree on the right with the integers 1-7 to make a binary search tree. Also, color each node "red" or "black" so that the tree also fulfills the requirements of a Red-Black tree.

Which nodes are red?

Note: Red-Black Trees are just one algorithm for self-balancing binary search tress. We have many more, including the AVL trees that we discussed last week.

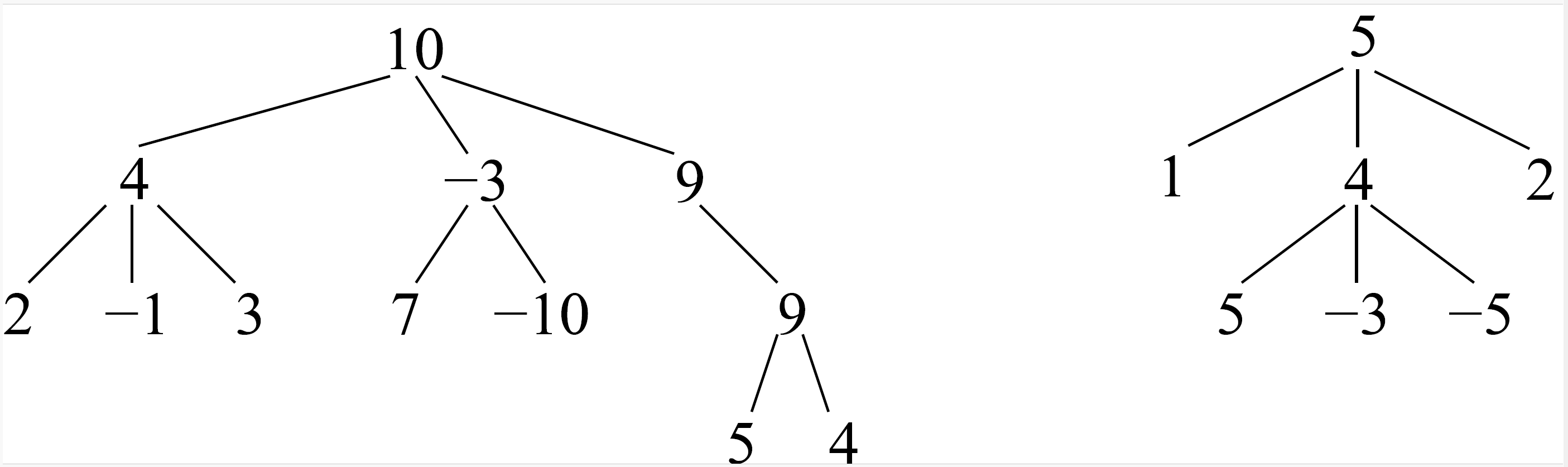
Trinary Tree

A trinary tree is similar to a binary tree except that each node has at most 3 children. Write a recursive function named EqualsChildrenSum that takes one argument, a pointer to the root of a trinary tree, and returns true if the value at each non-leaf node is the sum of the values of all of its children and false otherwise. In the examples below, the tree on the left will return true and the tree on the right will return false.

class Node {
  public:
    int value;
    Node* left;
    Node* middle;
    Node* right;
  };