CSCI-1200/lectures/21_trees_IV

Lecture 21 --- Trees, Part IV

Review from Lecture 20

• Breadth-first and depth-first tree search
• Increement/decrement operator
• Tree height, longest-shortest paths, breadth-first search
• Last piece of ds_set: removing an item, erase
• Erase with parent pointers, increment operation on iterators
• Limitations of our ds set implementatioN

Today’s Lecture

• Morris Traversal

21.1 Morris Traversal

Morris Traversal is a tree traversal algorithm that allows inorder (and also preorder) traversal of a binary tree without using recursion or a stack, achieving O(1) space complexity. It modifies the tree temporarily but restores it afterward.

Instead of using extra memory (like recursion stack or an explicit stack), Morris Traversal utilizes threaded binary trees by:

• Finding the inorder predecessor of the current node.

• Temporarily modifying the tree structure by creating threads (links) to the current node.

• Using these links to traverse back instead of a recursive call.

21.2 Morris Traversal - In Order

• Start from the root.

• If the left subtree is NULL, print the node and move to the right.

• If the left subtree exists, find the inorder predecessor (rightmost node in the left subtree):

• If the predecessor’s right child is NULL, set it to the current node (threading) and move left.

• If the predecessor’s right child points to the current node (thread already exists), remove the thread, print the current node, and move right.

• Repeat until you traverse the entire tree.

void inorderTraversal(TreeNode* root) {
        TreeNode *current=root;
        TreeNode *rightmost;
        while(current!=NULL){
            if(current->left!=NULL){
                rightmost=current->left;
                while(rightmost->right!=NULL && rightmost->right!=current){
                    rightmost=rightmost->right;
                }
                if(rightmost->right==NULL){ /* first time */
                    rightmost->right=current;
                    current=current->left;
                }else{  /* second time */
                    std::cout << current->val << " ";
                    rightmost->right=NULL;
                    current=current->right;
                }
            }else{  /* nodes which do not have left child */
                std::cout << current->val << " ";
                current=current->right;
            }
    }
    return;
}

You can test the above function using this program: inorder_main.cpp.

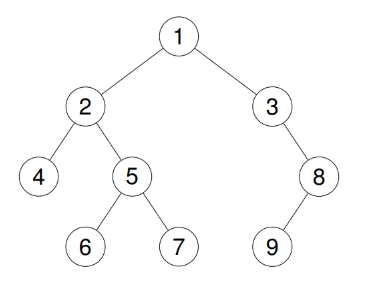
For this test case,

The testing program prints:

$ g++ inorder_main.cpp
$ ./a.out
Inorder Traversal using Morris Traversal:
4 2 6 5 7 1 3 9 8

Time and Space Complexity

• Time Complexity: O(N) (each node is visited at most twice)

• Space Complexity: O(1) (no extra space used except for modifying pointers)

21.3 Morris Traversal - Pre Order

To perform preorder traversal:

Print the node before going left instead of after restoring links.

void preorderTraversal(TreeNode* root) {
      TreeNode *current=root;
      TreeNode *rightmost;
      while(current != nullptr){
        if(current->left != nullptr){
            rightmost=current->left;
            while(rightmost->right!=nullptr && rightmost->right!=current){
                rightmost=rightmost->right;
            }
            if(rightmost->right==nullptr){ /* first time */
                std::cout << current->val << " ";
                rightmost->right=current;
                current=current->left;
            }else{  /* second time */
                rightmost->right=nullptr;
                current=current->right;
            }
        }else{  /* nodes which do not have left child */
            std::cout << current->val << " ";
            current=current->right;
        }
    }
    return;
}

You can test the above function using this program: preorder_main.cpp.

For above test case, the testing program prints:

$ g++ preorder_main.cpp
$ ./a.out
Preorder Traversal using Morris Traversal:
1 2 4 5 6 7 3 8 9

Time and Space Complexity

• Time Complexity: O(N) (each node is visited at most twice)

• Space Complexity: O(1) (no extra space used except for modifying pointers)

21.4 Morris Traversal - Post Order

Post order is different, and we need to write some helper functions here.

// function to reverse the right-edge path of a subtree
TreeNode* reverse(TreeNode* head) {
    TreeNode* prev = nullptr;
    TreeNode* next = nullptr;

    while (head != nullptr) {
        next = head->right;
        head->right = prev;
        prev = head;
        head = next;
    }
    return prev;
}

// function to traverse and collect nodes along a reversed right edge
void reverseTraverseRightEdge(TreeNode* head) {
    TreeNode* tail = reverse(head);
    TreeNode* current = tail;

    while (current != nullptr) {
        std::cout << current->val << " ";
        current = current->right;
    }
    reverse(tail); // restore the original tree structure
}

// Morris Postorder Traversal
void postorderTraversal(TreeNode* root) {
    TreeNode* current = root;
    TreeNode* rightmost;

    while (current != nullptr) {
        if (current->left != nullptr) {
            rightmost = current->left;
            while (rightmost->right != nullptr && rightmost->right != current) {
                rightmost = rightmost->right;
            }

            if (rightmost->right == nullptr) {
                rightmost->right = current;
                current = current->left;
            } else {
                rightmost->right = nullptr;
                reverseTraverseRightEdge(current->left);
                current = current->right;
            }
        } else {
            current = current->right;
        }
    }

    reverseTraverseRightEdge(root); // traverse the final right edge
    return;
}

You can test the above function using this program: postorder_main.cpp.

For above test case, the testing program prints:

$ g++ postorder_main.cpp
$ ./a.out
Postorder Traversal using Morris Traversal:
4 6 7 5 2 9 8 3 1