Lecture 19 --- Trees, Part II
Announcements
- Read the syllabus thoroughly for late days and extension policies -> https://www.cs.rpi.edu/academics/courses/spring24/csci1200/syllabus.php
Review from Lecture 18
- Binary Trees, Binary Search Trees, & Balanced Trees
- STL set container class (like STL map, but without the pairs!)
- Finding the smallest element in a BST.
- Overview of the ds set implementation: begin and find. (leetcode 700)
Today’s Lecture
- Warmup / Review: destroy_tree
- A very important ds set operation insert
- In-order, pre-order, and post-order traversal
- Finding the in-order successor of a binary tree node, tree iterator increment
19.1 Warmup Exercise
Write the ds set::destroy tree private helper function.
19.2 Insert
- Move left and right down the tree based on comparing keys. The goal is to find the location to do an insert that preserves the binary search tree ordering property.
- We will always be inserting at an empty (NULL) pointer location.
- Exercise: Why does this work? Is there always a place to put the new item? Is there ever more than one place to put the new item?
- IMPORTANT NOTE: Passing pointers by reference ensures that the new node is truly inserted into the tree. This is subtle but important.
- Note how the return value pair is constructed
- Exercise: How does the order that the nodes are inserted affect the final tree structure? Give an ordering that produces a balanced tree and an insertion ordering that produces a highly unbalanced tree.
19.3 In-order, Pre-order, Post-order Traversal
-
One of the fundamental tree operations is “traversing” the nodes in the tree and doing something at each node. The “doing something”, which is often just printing, is referred to generically as “visiting” the node.
-
There are three general orders in which binary trees are traversed: pre-order, in-order and post-order. In order to explain these, let’s first draw an “exactly balanced” binary search tree with the elements 1-7:
– What is the in-order traversal of this tree? Hint: it is monotonically increasing, which is always true for an in-order traversal of a binary search tree!
– What is the post-order traversal of this tree? Hint, it ends with “4” and the 3rd element printed is “2”.
– What is the pre-order traversal of this tree? Hint, the last element is the same as the last element of the in-order traversal (but that is not true in general! why not?)
-
Reminder: For an exactly balanced binary search tree with the elements 1-7:
- In-order: 1 2 3 (4) 5 6 7
- Pre-order: (4) 2 1 3 6 5 7
- Post-order: 1 3 2 5 7 6 (4)
-
Now let’s write code to print out the elements in a binary tree in each of these three orders. These functions are easy to write recursively, and the code for the three functions looks amazingly similar. Here’s the code for an in-order traversal to print the contents of a tree:
void print_in_order(ostream& ostr, const TreeNode<T>* p) {
if (p) {
print_in_order(ostr, p->left);
ostr << p->value << "\n";
print_in_order(ostr, p->right);
}
}
- How would you modify this code to perform pre-order and post-order traversals?
- What is the traversal order of the destroy_tree function we wrote earlier?
19.4 Tree Iterator Increment/Decrement - Implementation Choices
-
The increment operator should change the iterator’s pointer to point to the next TreeNode in an in-order traversal — the “in-order successor” — while the decrement operator should change the iterator’s pointer to point to the “in-order predecessor”.
-
Unlike the situation with lists and vectors, these predecessors and successors are not necessarily “nearby” (either in physical memory or by following a link) in the tree, as examples we draw in class will illustrate.
-
There are two common solution approaches:
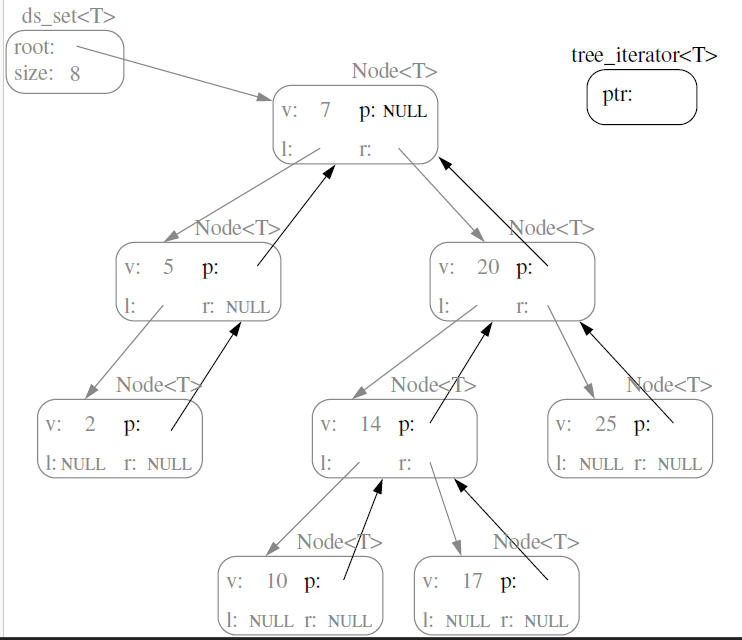
– Each node stores a parent pointer. Only the root node has a null parent pointer. [method 1]
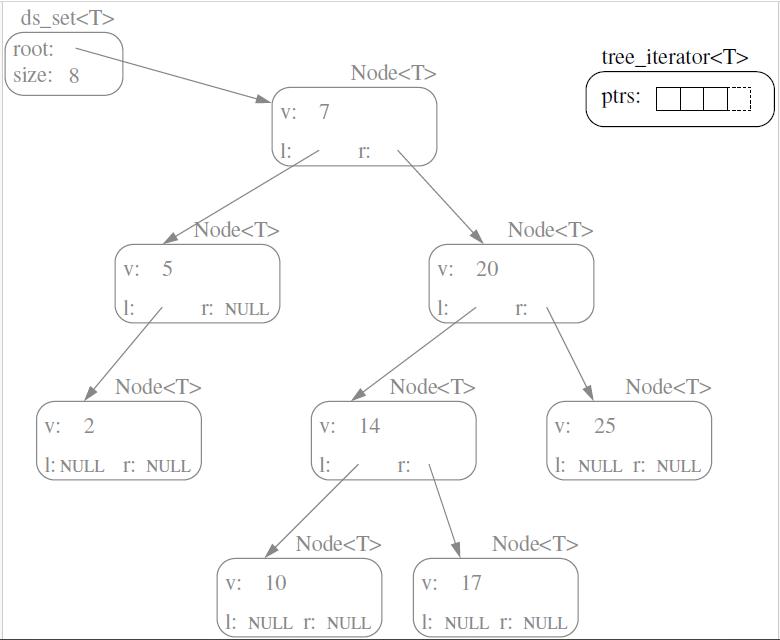
– Each iterator maintains a stack of pointers representing the path down the tree to the current node. [method 2]
-
If we choose the parent pointer method, we’ll need to rewrite the insert and erase member functions to correctly adjust parent pointers.
-
Although iterator increment looks expensive in the worst case for a single application of operator++, it is fairly easy to show that iterating through a tree storing n nodes requires O(n) operations overall.
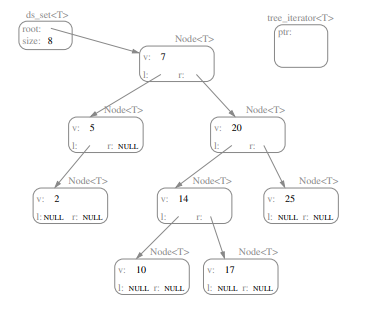
Exercise: [method 1] Write a fragment of code that given a node, finds the in-order successor using parent pointers.
Be sure to draw a picture to help you understand!
Exercise: [method 2] Write a fragment of code that given a tree iterator containing a pointer to the node and a
stack of pointers representing path from root to node, finds the in-order successor (without using parent pointers).
Either version can be extended to complete the implementation of increment/decrement for the ds_set tree iterators.
Exercise: What are the advantages & disadvantages of each method?
19.5 Limitations of Our BST Implementation
- The efficiency of the main insert, find and erase algorithms depends on the height of the tree.
- The best-case and average-case heights of a binary search tree storing n nodes are both O(log n). The worstcase, which often can happen in practice, is O(n).
- Developing more sophisticated algorithms to avoid the worst-case behavior will be covered in Introduction to Algorithms. One elegant extension to the binary search tree is described below...
19.6 B+ Trees
Unlike binary search trees, nodes in B+ trees (and their predecessor, the B tree) have up to b children. Thus B+ trees are very flat and very wide. This is good when it is very expensive to move from one node to another.
- B+ trees are supposed to be associative (i.e. they have key-value pairs), but we will just focus on the keys.
- Just like STL map and STL set, these keys and values can be any type, but keys must have an operator< defined.
- In a B tree key-value pairs can show up anywhere in the tree, in a B+ tree all the key-value pairs are in the leaves and the non-leaf nodes contain duplicates of some keys.
- In either type of tree, all leaves are the same distance from the root.
- The keys are always sorted in a B/B+ tree node, and there are up to b − 1 of them. They act like b − 1 binary search tree nodes mashed together.
- In fact, with the exception of the root, nodes will always have between roughly b/2 and b − 1 keys (in our implementation).
- If a B+ tree node has k keys key0, key1, key2, . . . , keyk−1, it will have k + 1 children. The keys in the leftmost child must be < key0, the next child must have keys such that they are ≥key0 and < key1, and so on up to the rightmost child which has only keys ≥keyk−1.